Naushonia tinkeri, Alvarez, Iliffe & Villalobos, 2017
|
publication ID |
https://doi.org/10.11646/zootaxa.4258.2.8 |
|
publication LSID |
lsid:zoobank.org:pub:A3869000-9B69-4680-8CBB-297040410BD3 |
|
DOI |
https://doi.org/10.5281/zenodo.6000475 |
|
persistent identifier |
https://treatment.plazi.org/id/03A387D0-FFE6-D677-4892-FD35A24EFAEC |
|
treatment provided by |
Plazi |
|
scientific name |
Naushonia tinkeri |
| status |
sp. nov. |
Naushonia tinkeri View in CoL sp. nov.
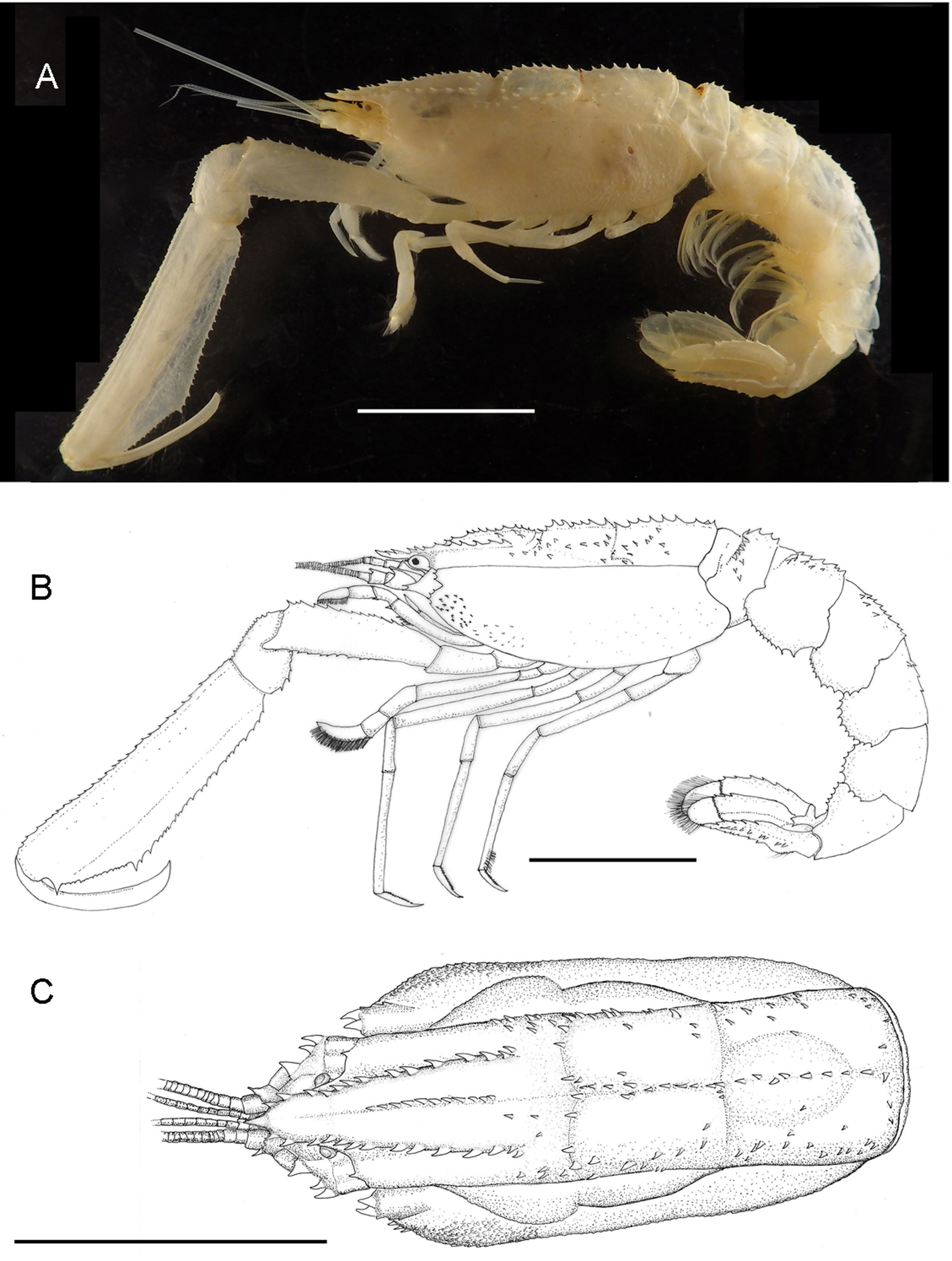
( Figs. 1–3 View FIGURE 1 View FIGURE 2 View FIGURE 3 )
Type material. Holotype male, cl 19.3 mm, tl 43.5 mm; Dan’s Cave (26°15ꞌ N, 77°11ꞌ W), depth 18 m, near cave entrance, under the halocline in marine water; Great Abaco, the Bahamas; coll. B. Kakuk; 9 Dec. 2013; CNCR 31879 . Paratype male, cl 19.5 mm (broken), tl 47.8 mm, Sawmill Sink (26°13ꞌ N, 77°13ꞌ W), depth 26 m, beneath the halocline and under a dense cloud of hydrogen sulfide in marine water; Great Abaco, the Bahamas; coll. B. Kakuk; 1 May 2008; CNCR 31880 .
Description. Carapace subcylindrical, about 0.4 of total length, with three clearly marked sections: cephalic, gastric and cardiac, divided by well-marked cervical and cardiac grooves ( Fig. 1 View FIGURE 1 A, B). Linea thalassinica clearly separating dorsal from lateral portions of carapace. Rostrum reaching distal section of third article of antennular peduncle, with three strong spines anterior to orbit; rostral margin with eight strong spines from orbit to cervical groove; dorsal surface of rostrum devoid of spines, slightly concave. Anterior margin of carapace with two spines below linea thalassinica next to antennal peduncle, pterygostomial angle with six spines ( Fig. 2 View FIGURE 2 A). Dorsal surface of carapace with discontinuous median ridge, with 11, 10 and 9–10 spines on cephalic, middle/gastric and cardiac portions, respectively ( Fig. 1 View FIGURE 1 C).
Pleon about 1.7 times carapace length. First somite shortest, with row of spines along dorsal surface, middorsal ridge with four strong spines, ventral margin partially covered by carapace. Second somite with mid-dorsal ridge formed by six or seven spines, few scattered spines present on dorsal anterior margin and next to mid-dorsal ridge; toothed ventrolateral margin, largest tooth on posterior portion. Third somite with mid-dorsal ridge formed by row of spines, with few additional scattered spines; ventrolateral margin toothed, teeth of similar size. Fourth somite with few spines along mid-dorsal surface; ventrolateral margin armed with similar-sized teeth. Fifth and sixth somites without spines on dorsal surface; ventrolateral margins armed with similar-sized teeth.
Telson 1.4 times as long as wide. Lateral margins of anterior half subparallel, smooth; posterior half rounded with 14–16 marginal teeth of uniform size interspersed with setae ( Fig. 2 View FIGURE 2 B). Dorsal surface with strong anterior spine on middle portion, central portion elevated with scattered spines, mid-dorsal ridge faintly marked.
Eyes normally developed, occupying orbit completely, pigmented with loosely arranged dark granules, visible in lateral and dorsal views; anterior surface with prominent conical projection ( Figs. 1 View FIGURE 1 C, 2A).
Antennule with first article shorter and thicker, bearing acute spines on distal margin. Second article with spine-like projection on distal margin of mesial surface. Third article slender and longer than other two combined.
Antenna with scaphocerite reaching third article of antennular peduncle. External margin with large spine projecting beyond distal margin of blade, lateral margin with one or two spines ( Fig. 3 View FIGURE 3 D). Peduncle robust, second article with four spines on distal margin, three visible in ventral view; third to fifth articles each with one large spine on distal margin ( Fig. 2 View FIGURE 2 F).
Mandible with molar and incisor processes forming cavity to receive palp. Molar process with blunt margin, incisor process with nine small teeth. Palp 2-articulated, densely setose along external margin, distal article digitiform ( Fig. 2 View FIGURE 2 C).
Maxillule with 2-articulated palp, proximal article with tuft of setae near base, distal article devoid of setae ( Fig. 2 View FIGURE 2 E). Anterior lacinia slender, distal portion becoming wider, margin bearing setae. Posterior lacinia of irregular shape, approximately trapezoidal, with setae along anterior margin, increasing in size distally, small less dense field of setae on posterior margin ( Fig. 2 View FIGURE 2 E). Anterior and posterior lacinia clearly separated, not overlapping.
Maxilla with elongate digitiform palp, bearing long marginal setae ( Fig. 2 View FIGURE 2 D). Distal endite bilobed, shorter than palp, with distal marginal setae. Medial endite slender, digitiform, with short setae on distal margin. Proximal endite approximately trapezoidal, with submarginal rows of spines, distal margin bearing long setae. Scaphognathite three times as long as wide, anterior lobe wide, oval-shaped, bordered with long setae; posterior lobe subtriangular, elongate, distal end truncate with 10 long, simple setae ( Fig. 2 View FIGURE 2 D).
First maxilliped with subrectangular basis. Palp oval-shaped, internal margin and internal half densely covered with setae ( Fig. 2 View FIGURE 2 G). Endopod biarticulated, distal article oval-shaped, margin covered with setae. Exopod biarticulated, basal article expanded to form "caridean" lobe, distal margin broadly rounded with long setae; second article elongate, flagellum with long setae, longer than second article. Epipod large, subrectangular.
Second maxilliped with endopod composed of five articles, proximal two articles with long plumose setae, third article shortest, distal article wider than others, with long plumose setae ( Fig. 2 View FIGURE 2 H). Exopod biarticulated, proximal article about three times as long as distal, flagellum with setae, increasing in size distally. Epipod in form of subtriangular laminar expansion, inferior margin with small spines. Podobranch large, central axis longer than epipod.
Third maxilliped ( Fig. 3 View FIGURE 3 A) pediform. Endopod subdivided into six articles; basis short, with tuft of setae on external margin; ischium with long setae, spine on external distal margin; merus slightly curved, longer than ischium, with scattered setal fields; carpus short, with longitudinal row of setae along external margin; propodus thicker distally with row of setae along internal margin, subequal in length to carpus; dactylus thicker than remaining articles, with dense, uniform row of setae along gnathal border, rest of article with scattered long setae. Exopod biarticulated, basal article longer than basis and ischium of endopod combined, with scattered setae; distal article about 0.33 length of proximal one. Epipod in form of triangular laminar expansion, inferior margin with irregularly spaced spines; podobranch well-developed.
First pereiopods subchelate, subequal in size, strong, about 0.65 of total length of individuals ( Figs. 1 View FIGURE 1 A, 3B). Coxa with prominent acute tooth on ventral margin. Ischium about 0.33 length of merus, triangular in section, internal margin with row of seven spines, distal width 2.2 times proximal one. Merus 2.1 length of carpus, triangular in section, forming three longitudinal ridges, ventral ridge armed with minute spines, dorsal ridge with larger spines, rounded projection on distoventral margin overlapping carpus on middle section. Carpus short, wide; dorsal margin with proximal notch, rounded; dorsal and ventral margins armed with sharp spines, additional field of spines present on mesial surface. Propodus longest of all articles, 3.4 times as long as wide; 5, 1.6 and 3.5 times length of ischium, merus and carpus, respectively; triangular in section, longitudinal ridges armed with sharp spines; internal surface inflated; cutting edge lined with small teeth in addition to one large tooth adjacent to propodo-dactylar articulation. Dactylus 0.6 length of propodus, slender, curved; cutting edge lightly granulated, with scattered setae.
Second pereiopods stout, short, about 0.4 length of first pereiopod, not chelate ( Fig. 1 View FIGURE 1 A, B). Ischium and propodus shortest articles. Merus longest article, 0.4 total length of pereiopod. Propodus densely setose. Dactylus lanceolate, densely setose along external and internal margins, latter finely serrate ( Fig. 3 View FIGURE 3 F).
Third to fifth pereiopods similar in shape, third longest ( Fig. 1 View FIGURE 1 B). Third pereiopod with merus being longest article; propodus second longest article, 0.8 length of merus; ischium, carpus and dactylus subequal in size; dactylus slender ( Fig. 3 View FIGURE 3 G), ending in acute, curved tip, distal 0.65 of internal margin finely serrate, external margin with scattered spines on distal third. Fourth pereiopod similar to third, merus and propodus subequal in length; dactylus ( Fig. 3 View FIGURE 3 H) ending in acute tip, internal margin finely serrate, external margin with irregularly spaced large spines. Fifth pereiopod shorter than fourth, propodus with distal tuft of setae; dactylus ( Fig. 3 View FIGURE 3 I) ending in acute tip, internal margin finely serrate, external margin with one simple seta on distal 0.65 of its length.
Etymology. The specific epithet is named in honor of Dr. Keith Tinker, Director of the Antiquities, Monuments and Museum Corporation (AMMC) of the Bahamas. Over the last 20 years, Dr. Tinker has established and funded programs within the National Museum of the Bahamas specifically dedicated to the exploration and archaeological, paleontological and biological exploration and research in the blue holes and underwater caves of the Bahamas. This research culminated in the two sites listed in the present paper being included in a newly designated 34,000 acre blue holes conservation area, the highest degree of protection for any government lands in the Bahamas.
Distribution. The new species is known only from two anchialine caves on Great Abaco Island (Little Bahama Bank) in the northern Bahamas.
Habitat. Dan’s Cave and Sawmill Sink are extensive anchialine caves with nearly 20 km of mapped subterranean passageway. The entrances are separate by 3 km and each entrance is at least 1 km from the nearest coastline. Specimens were collected from small burrows within compacted, organic peat deposits of each cave. Both specimens were found within 40 m of the cave entrances, just below the halocline.
Remarks. The new species described herein is closest morphologically to Naushonia augudrea ( Juarrero & García, 1997) from Holguín Province in eastern Cuba, with which it shares the carapace with cervical and cardiac grooves, and a similar spination pattern, as well as the toothed ventrolateral margins of pleura. In fact, N. tinkeri n. sp. and N. augudrea are the only two known species of Naushonia with a carapace possessing both cervical and cardiac grooves. Despite their great overall similarity, N. tinkeri n. sp. can be distinguished from N. augudrea by the pigmented cornea, a first pereiopod with a more slender propodus (length/width ratio: 3.07 vs 2.41) and a dactylus without teeth on its external margin, and the telson longer relative to the uropod length (telson length/ exopod length: 0.83 vs 0.60) ( Juarrero et al. 1997).
Naushonia manningi Alvarez, Villalobos & Iliffe, 2000 , also described from an anchialine cave in the Bahamas, has some morphological resemblance to the new species, e.g. in the shape and size of the first pereiopod and the toothed ventrolateral margins of pleura 2–6. However, the carapace of N. manningi has only one - cervical groove. Noteworthy, N. tinkeri n. sp. and N. manningi both present a sharp, prominent tooth on the ventral surface of the first pereiopod coxa ( Fig. 3 View FIGURE 3 D), a character that is only shared with N. japonica Komai, 2004 from Japan ( Komai 2004). It is not unusual to find morphological similarities among species of Naushonia from different geographic areas. Anker (2014) stated that N. draconis from Guadeloupe Island in the French Antilles (now also known from Cuba; Komai & Anker 2015) is most similar to N. palauensis ( Alvarez, Villalobos & Iliffe, 2010) from Palau; whereas Komai & Anker (2010) compared, because of their similarity, N. latimana Komai & Anker, 2010 , from Mayotte Island and N. serratipalma Komai & Anker, 2010 , from the French Polynesia with N. perrieri (Nobili, 1904) from Djibouti and N. japonica from Japan. This pattern is usually associated with groups having an ancient origin, e.g. Cretaceous or even older, in which the original stock started to differentiate in the Tethys Ocean.
Komai & Anker (2015) published a key to all 14 species of Naushonia known at that time, also providing a full redescription of the previously poorly known N. portoricensis (Rathbun, 1901) along with new data on some other taxa making a new key rather unnecessary. Naushonia tinkeri n. sp. can be keyed out to couplet 4 (leading to N. augudrea ), and from there as follows: 4a: cornea unpigmented, dactylus of first pereiopod with toothed external margin, telson as long as wide, 0.6 times length of endopod of uropod— N. augudrea ; 4b: cornea pigmented, dactylus of first pereiopod with external margin smooth, telson 1.4 times as long as wide, 0.9 times length of endopod of uropod— N. tinkeri n. sp.
No known copyright restrictions apply. See Agosti, D., Egloff, W., 2009. Taxonomic information exchange and copyright: the Plazi approach. BMC Research Notes 2009, 2:53 for further explanation.
|
Kingdom |
|
|
Phylum |
|
|
Class |
|
|
Order |
|
|
Family |
|
|
SubFamily |
Naushoniinae |
|
Genus |