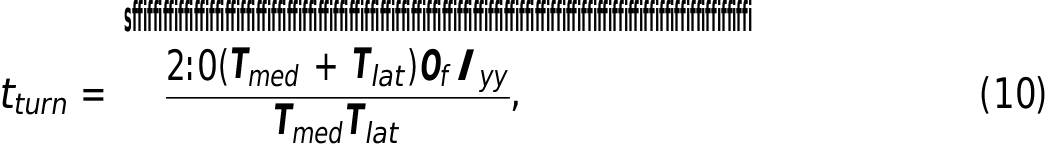Tyrannosaurus rex, Osborn, 1905

John R. Hutchinson, Victor Ng-Thow-Hing & Frank C. Anderson, 2007, A 3 D interactive method for estimating body segmental parameters in animals: Application to the turning and running performance of Tyrannosaurus rex, Journal of Theoretical Biology 246 (4), pp. 660-680 : 665-678

2.3 . Tyrannosaurus skeletal geometry acquisition

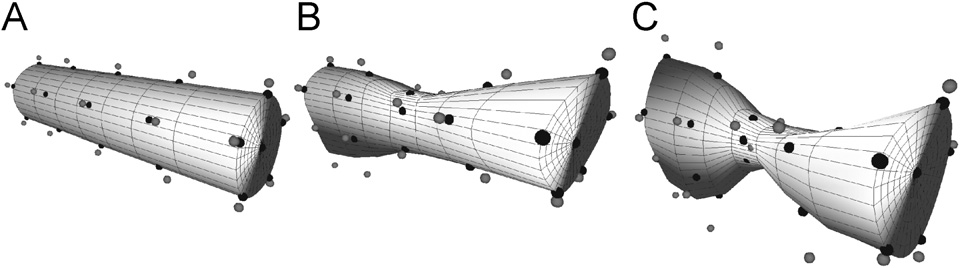
We chose Museum of the Rockies Tyrannosaurus rex specimen MOR 555 because a good cast of this nicely preserved specimen ( Fig. 5A ) was available next to the University of California Museum of Paleontology (Berkeley, California). This location had enough space for us to set up a three-dimensional (x; y; z) coordinate system for estimating body dimensions. The coordinate system was constructed by laying down a straight 10 m line on the floor near the skeleton, forming the x -axis (craniocaudal; parallel to the body). A total of 67 landmark points on the skeleton ( Fig. 5B ) were marked to represent the outline of the skeleton from tail to snout (total axial length = 10.8 m). Next, for each point the height (y -axis, with 0 at the floor) was measured using a plumb bob and measuring tape. The coordinates in the x–z (horizontal) plane were measured from the point where the plumb bob contacted the ground when hanging still to the coordinate axes. This simple approach can be used quickly and easily with mounted specimens in most museums. As the skeleton was not oriented in a straight line, the coordinates needed to be straightened out by transforming them so that the midline dorsal points all lay along the same craniocaudal line, which was redefined as the new x -axis. Because the left and right sides of the mounted cast were not symmetrical as in life, we adjusted the z -axis values to be the mean of the measured left/right values. Additionally, as the mouth was open in the cast, we took skull measurements to close the mouth in our model.

Limb bone geometry was acquired in a previous study ( Hutchinson et al., 2005). The pelvis and hindlimbs were represented in the model as realistic 3D surfaces, each made of several thousand polygons. Joints connecting those bone segments were likewise defined as in the latter study. This 3D limb bone model was connected to the body model by placing its hip joint center at the same location as the centroid of the acetabulum in the mounted skeleton, which we also collected landmark points for.

As Fig. 5B shows, the skeletal landmark points we collected were insufficient to accurately describe the shape of the animal, as they did not account for the curvature of the soft tissues. Naturally, use of these landmarks alone would drastically underestimate body mass (see below). We used our B-spline solid modeling software to assist us in representing the changes of body shape caused by soft tissue ( Fig. 2 ).

2.4. Tyrannosaurus fleshed-out body model

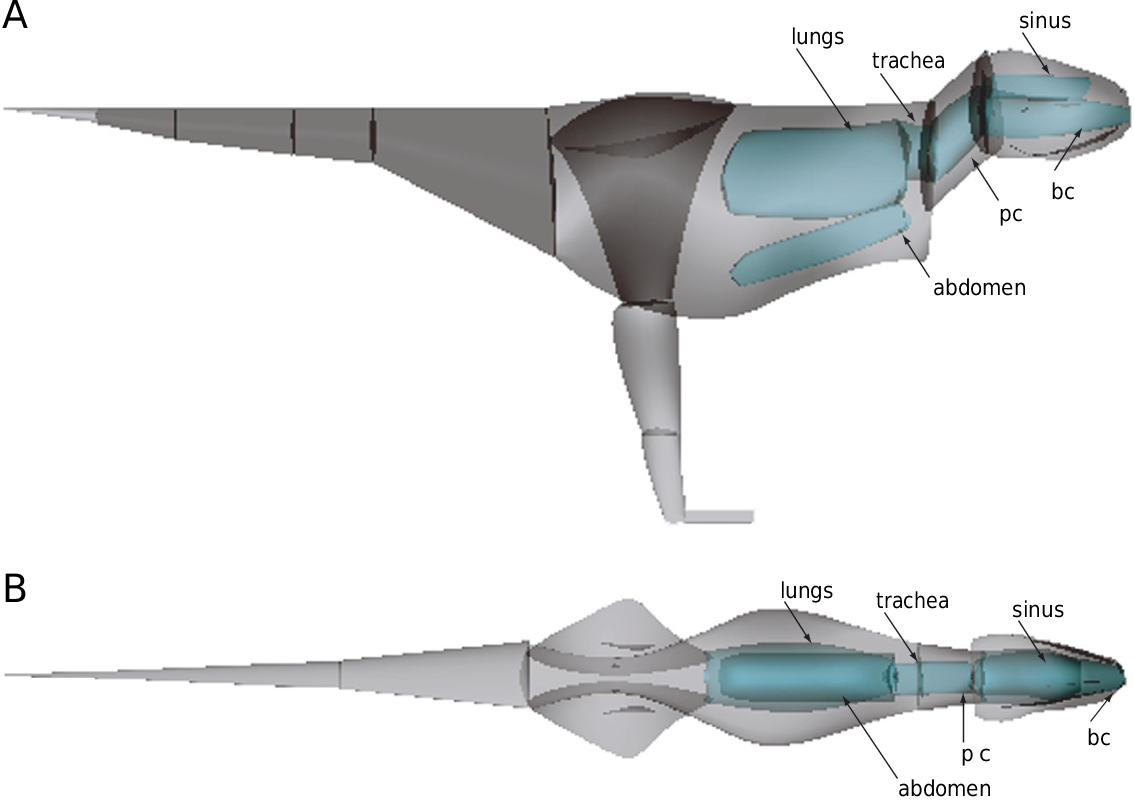
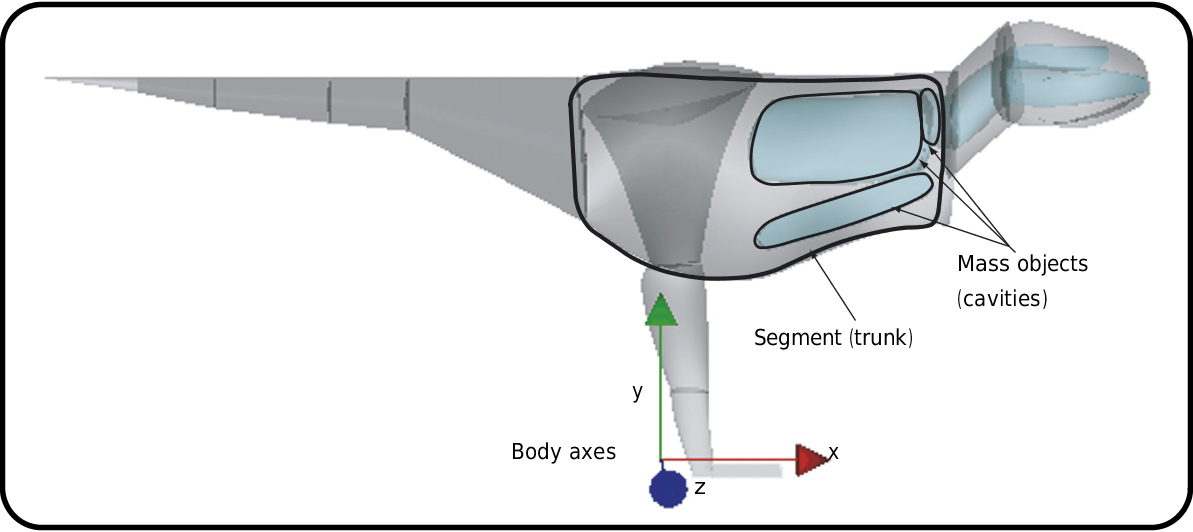
We first separated our model into a ‘torso’ set: a head, a neck, a trunk, and five tail segments corresponding to the underlying skeletal data described above. Second, we had two ‘leg’ sets, each consisting of four smaller segments: the thigh, shank, metatarsus, and pes. Hence, our model (torso plus leg segment sets) had a total of 16 body segments. We then created our original model (referred to here as Model 1) to estimate Tyrannosaurus body dimensions by fleshing out the skeletal data. To show how much this fleshing out procedure changed the mass set values, we also calculated mass sets for the torso by only using the skeletal landmark points as the edges of the body (as we did for the ostrich).

Fleshing out the skeleton was an eloquent reminder to us how much artistic license is inevitably involved. Importantly, we did not check the resulting mass set data as we fleshed out the skeleton, as that might introduce bias toward some mass set values. We merely attempted to reconstruct what we thought the entire body dimensions should look like for a relatively ‘skinny’ (minimal amount of flesh outside the skeleton, averaging just a few centimeters) adult Tyrannosaurus , using the skeleton and our experience as animal anatomists to guide us. B-spline solid shapes (cylinders, spheres, or ellipses depending on the segment) were first shrinkwrapped to the underlying skeleton and then individual points were moved away from the skeleton to symmetrically add the amount of flesh desired. Brief reference to other representations in the literature (especially Paul, 1988, 1997; Henderson, 1999) was used only in the final smoothing stages to ensure that the body contours were not exceptionally unusual.

Several simplifications were involved. We did not aim for extreme anatomical realism, incorporating every externally visible ridge and crest of the underlying skeleton. We omitted detailed representation of the arm segments. Rather, we added a small amount of volume at the cranial ends of the coracoids to represent the tiny arms. Likewise, we did not detail the pes segment. A simple rectangular block (matching the rough dimensions of digit 3; Hutchinson et al., 2005) was used to represent the pes, and assigned a mass of 41 kg based upon scaling data for extant taxa ( Hutchinson, 2004a, b). The pes was considered fused to the ground and hence not used to calculate whole body CM or inertia values. Both omissions are justifiable as the small masses of these segments would have minimal effects on the mass set calculations. Our goal was to construct a reasonable—and most importantly, simple and flexible enough for sensitivity analysis—initial representation of the body outline in 3D which could be made more realistic in the future as desired.

The model (and all later modifications thereof in our sensitivity analysis, except where noted) was constructed and kept in a single, completely columnar reference pose (as in Hutchinson et al., 2005) with all leg segments vertically aligned, except that the hip joints were kept abducted by 15 ° in order to properly place flesh around the thighs and to match expected hip abduction in theropods (e.g., Paul, 1988; Hutchinson et al., 2005). This is important as the leg segment positions influence the total body mass set. Fig. 6 shows the original model.

2.5. Body segment densities

One of the most important assumptions involved in body mass estimates for extinct animals is the average density of various body segments. Most studies have assumed a homogeneous density throughout all or most body areas (e.g., Alexander, 1985, 1989; Paul, 1997; Henderson, 1999; Motani, 2001; Henderson and Snively, 2003) except usually including zero-density lungs, ranging 8–10% of body volume or up to 15% of trunk volume. Such assumptions also have bearing on the CM positions and inertia magnitudes. Henderson (2003b); Henderson (2006) has more cautiously entered varying densities for sauropod neck and trunk segments.

Our model offers the advantage of being easily able to incorporate as much or as little variation of density within/ among body segments as desired, and of having such variation represented by anatomically realistic shapes. High-resolution data from computed tomography, dense point clouds, or other complex geometric shapes can be imported into the model framework. Hence, a model can be as simple or complex as one desires, within hardware limitations.

For our model of T. rex , we began by assigning all segments a density equal to water (1000 kg m ‒ 3) as did many previous authors ( Alexander, 1985; Henderson, 1999). We then embedded (as per above) simplified but anatomically appropriate shapes to represent zero-density cavities inside several segments. These cavities were placed with reference to osteological indicators of pulmonary anatomy ( O’Connor and Claessens, 2005; O’Connor, 2006) in Tyrannosaurus . The head segment included a buccal cavity and ‘sinus’ (antorbital and surrounding cranial sinuses; Witmer, 1997); we shaped these to roughly match the skull cavities of the specimen. The neck segment had a pharyngeal cavity (= trachea, esophagus, associated air sacs; O’Connor and Claessens, 2005; O’Connor, 2006), whereas the trunk segment had three cavities: ‘trachea’ (continuation of pharyngeal cavity), ‘lungs’ (and associated air sacs), and ‘abdomen’ (clavicular and thoracic air sacs; O’Connor and Claessens, 2005). Fig. 6 shows the cavity shapes we used. The volumes of these cavities and the final densities of the segments containing them are shown in Table 3 .

2.6. Sensitivity analysis

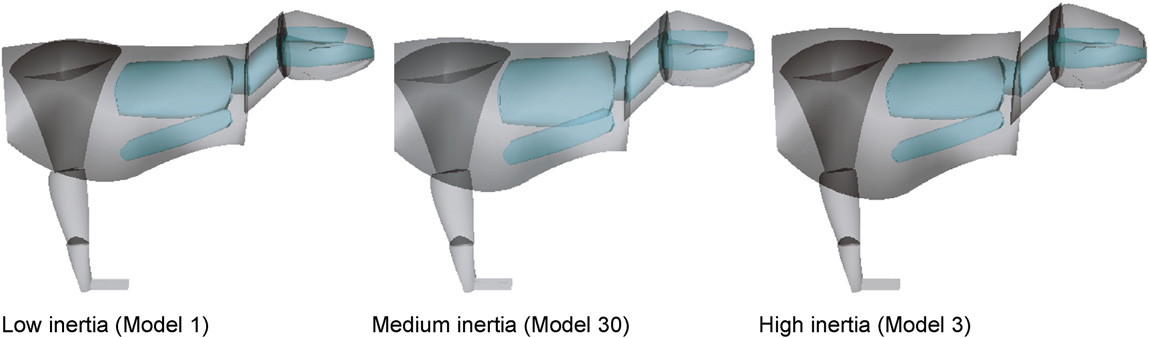
We created 29 new Tyrannosaurus models as variations of our original model (Model 1) by altering the original torso segment set, embedded cavity, and leg dimensions ( Fig. 7 ). Only B-spline solid shapes were changed, not the underlying skeleton. Body segments (along with their embedded cavities) were either left in their original state or increased along their y - and z -axes (vertical and mediolateral) by 10% or 21% (10% twice); i.e., volumes and masses increased by 1.21 or 1.46 X. This was done because our original model was designed to be a minimal estimate of mass sets; we presumed the real animal would have had more soft tissue. We also separately increased the neck and trunk embedded cavity dimensions by 10% or 21%, checking to ensure that these cavities were not excessively penetrating our skeletal landmark points. Head segment cavities did not require enlargement as their dimensions were set by those of the skull cavities. The leg segments were increased by 10% or 21% along their x - and z - axes (craniocaudal and mediolateral) to represent more muscular legs. The mass of the pes segment was not changed as this was deemed sufficiently large. Consequently, we made 26 models of the body of Tyrannosaurus (Models 2–27) to consider all combinations of one or more of these variations from Model 1. To investigate how much different tail dimensions (independently from the rest of the body) changed mass set values, we added a model (#28) with tail dorsovental and mediolateral dimensions increased by 21%. As tail position could have influence our mass set results, we made an additional model (#29) with a tail in a more ventral, sloped orientation (tail depressed ventrally by ~ 25 °; this required deforming the tail segments slightly, boosting mass by ~ 3%). Finally, we constructed our intuitive ‘best guess’ model (#30) with a tail volume enlarged by 1.46 X as in Model 28, the body and leg volumes increased by 1.21 X, and body cavities enlarged by 1.46 X. Once all 30 models were finished, we tabulated their mass set values to examine the effects of different assumptions about body segment shapes and sizes ( Table 4 , Fig. 8 ).

2.7. Turning speed of T. rex

To illustrate the importance of moment of inertia in dynamic movements, we estimated the minimum time required for T. rex to execute a stationary turn of its trunk, neck, and head by 45 ° to the right (clockwise) while standing only on its right foot. We assumed that the tail during this movement would not move with the trunk. Therefore, the turning mass set included the trunk starting from just behind the pelvis at the base of the tail, the left hindlimb, the neck, and the head ( Fig. 9 ). We further assumed that the optimal strategy for a minimum-time turn (to the right) would be to turn the right medial (internal) rotator muscles on maximally to initiate the turn and then the right lateral (external) rotators on for decelerating the turn to a stop at the final angle. The T. rex began at rest in a forward facing position (O i = 0:0 Q; ̇O i = 0: 0 Q / s) and terminated facing 45 ° to the right also at rest (O f = 45:0 Q; ̇ O f = 0:0 Q / s). Allowing for the fact that the maximal medial rotation and lateral rotation hip joint moments were not likely the same, a formula for the time required by the movement is given by where tturn is the time it takes to execute the turn, O f is the final medial rotation angle of the right hip, T med and T lat are the estimated maximum medial and lateral hip joint moments, respectively, that can be generated by T. rex , and Iyy is the moment of inertia of the rotating body mass about the right hip joint.

sffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi 2: 0(T med + T lat) O f I yy tturn =, (10) T med T lat

The maximum hip rotation moments were estimated based on the forces exerted by long-axis (i.e., medial and lateral) rotator muscles crossing the hip joint times the moment arms of those muscles ( Hutchinson and Gatesy, 2000; Carrano and Hutchinson, 2002). We estimated the forces using scaled physiological cross-sectional areas and fascicle lengths for the muscles (data from Hutchinson, 2004a, b). The areas were estimated as follows. First we assumed that 4% or 5% of body mass was the mass of the hip extensors, which is toward the upper end of their size in extant bipeds such as humans and ostriches ( Hutchinson, 2004a) but deemed quite feasible in our initial whole body model (see muscle mass estimation for running ability below). Hip lateral rotators were assumed to match this mass, which our musculoskeletal model ( Hutchinson et al., 2005) supports; most hip extensors also have lateral rotation moment arms as they insert lateral to the medially offset femoral head. We then assumed that the mass of hip flexors was 50% of this mass, which is within the range of data for extant bipeds (dissections from Hutchinson, 2004a; flexors were ~ 50–75% of extensor mass). Again we assumed that the medial rotator mass was the same as the hip flexor mass, also supported by the musculoskeletal model. By dividing these masses by muscle fascicle lengths (using four scaling estimates from Hutchinson, 2004b: Table 3 ; assuming flexor and extensor fascicles to be of equivalent length) we then estimated muscle physiological cross-sectional areas (assuming pennation angles to be negligible, which is reasonable for most hip muscles and unlikely to be an error> 10%). We calculated maximal muscle forces assuming a maximal isometric muscle stress of 3.0 X 10 5 N m ‒ 2 (explained in Hutchinson, 2004a, b). Finally we used the mean moment arms (across the maximal range of motion of the hip joint) for the medial and lateral rotators (from the 3D Tyrannosaurus musculoskeletal model from Hutchinson et al., 2005) to calculate the maximal medial and lateral rotation moments. The values entered in these calculations are in Table 6 .

Using the parallel axis theorem ( Marion, 1970), the moment of inertia for the rotating mass set is given by where Iyy is the moment of inertia about a vertical axis passing through the hip joint, I yy com the moment of inertia about the vertical axis passing the CM of the rotating mass set, m the mass of the rotating mass set, and rcom the distance from the right hip joint center to the CM of the rotating mass set. All inertial parameters in Eqs. (10) and (11) were estimated using our mass set software. Estimates of turning time were computed for the different combinations of low, medium, and high estimates of the medial and lateral joint moments with low (Model 1: original), medium (Model 30: ‘best guess’ intermediate model), and high (Model 3: torso enlarged 1.46 X) estimates of moment of inertia. Additionally, the same combinations were performed with the moment of inertia about the CM neglected (i.e., I yy com = 0: 0). These values are shown in Table 6 .

I = I com + mr 2 (11) yy yy com

2.8. Running ability of T. rex

To investigate how more realistic estimates of segment mass and CM could change previous estimates of the running speed of Tyrannosaurus , we replaced segment mass and CM data assumed in Hutchinson (2004b) with our mass set data. We used data from our original ‘skinny’ model (#1), the model with 21% larger embedded cavities (#21), the model with 21% wider and thicker legs (#23), and our ‘best guess’ model (#30). Additionally we used our original model to estimate how much further forward the trunk CM might have moved if the left hip joint was flexed (in swing phase) by 65 ° forward of vertical, as an extreme case ( Hutchinson, 2004b). We then re-calculated the muscle masses needed to support the right limb at mid-stance during relatively fast running, with a vertical ground reaction force (GRF) of 2.5 times body weight ( Hutchinson, 2004a, b). That biomechanical model was posed in the ‘‘Trex_1’’ bent-legged pose ( Hutchinson and Garcia, 2002). Realistic pose-specific muscle moment arms ( Hutchinson et al., 2005) were used along with the other model data presented in Hutchinson (2004b) to calculate the minimal extensor muscle masses required to be actively contracting about the right hip, knee, and ankle.

From these masses, we finally calculated what maximal vertical GRF the limb could support. We did this by estimating the extensor muscle mass able to support each joint from the mass of the respective limb segment. The bulk of the hip and knee extensors would have been located in the thigh segment, whereas ankle extensors would have been concentrated in the shank segment ( Carrano and Hutchinson, 2002). However, those muscles would have only been some fraction of the segments’ total masses, not the entire mass. To estimate that fraction, we calculated the fractions of segment mass that homologous muscles occupy in extant non-avian Reptilia ( Iguana , Basiliscus , and Alligator ) and birds ( Eudromia , Gallus , Meleagris , Dromaius , and Struthio ), using the data from Hutchinson (2004a). As a reasonable starting assumption, we took the average fraction of extensor muscle/segment mass for the ‘reptiles’ and for the birds. These fractions were then multiplied by the estimated segment masses for Tyrannosaurus to calculate its likely extensor muscle masses (in absolute terms and as percentages of body mass).

The average of the non-avian Reptilia plus the average of the bird fractions were used for all muscle masses except for the knee extensors. The skeleton demonstrates that the knee extensor muscles in bipedal Tyrannosaurus were much closer to the avian than the basal reptilian condition ( Carrano and Hutchinson, 2002), so only the average of the bird fractions was used to calculate the knee extensor muscle mass (the non-avian Reptilia fraction was smaller). For the remaining muscles, it is less certain how derived they were relative to basal reptilian muscles, so an average, intermediate condition was our objective assumption. Considerable variation exists in extant taxa, so our approach can be no better than a rough estimate.

To see how closely each joint’s estimated extensor muscle mass was matched to the mass required for fast running, we divided the extensor muscle mass estimated to have been present (from this study; above) by the extensor muscle mass required (from the model of Hutchinson, 2004b), for the hip, knee, ankle and toe. Finally, as the limb could not support a higher GRF than its weakest joint could, we multiplied the lowest of these ratios (muscle mass present vs. required) by 2.5 to estimate the maximum supportable vertical GRF in multiples of body weight.

All input and output data not reported in the references cited above are shown in Section 3 ( Tables 8 and 9 ).

3. Results

3.1. Ostrich validation

Our validation of the model with sensitivity analysis on an ostrich cadaver/skeleton model showed some of the inaccuracies of our approach, but still bolstered the utility of our modeling procedure to estimate mass parameters for extinct animals ( Table 2 ). Generally our results matched our expectations; the carcass and fleshed-out models gave estimates closer to the ‘real’ mass value whereas the skeletal model’s mass estimate was lower (77% of the actual value). If densities had been assumed to be 1000 kg m ‒ 3, rather than taken from the actual carcass (888 kg m ‒ 3; similar to the 850 kg m ‒ 3 assumed for an emu by Seebacher, 2001), the results would have been overestimated because the presence of low-density air sacs was neglected. Estimates of the trunk CM position were within 2, 6, and 4 cm of the experimental values for the x, y, and z coordinates, respectively. These absolute deviations represent 2.4%, 15%, and 21% errors relative to the total size dimensions of the trunk (0.83, 0.39, 0.19 m). Also somewhat surprisingly, the skeleton model had the closest matches to the Iyy and Izz measured values (within 133% and 90%, respectively), whereas the fleshed-out model had the closest match to the empirical Ixx value (within 95%). The model made from digitizing the actual carcass did not perform the best out of all three estimates of the trunk moments of inertia about the CM, although its estimates of the Iyy and Izz values were better than those of the fleshed-out model. Some of the deviations between the experimental measurements and B-spline estimates could be due to inaccuracies in the experimental measures. While the experimental techniques for locating the CM of a body can be quite accurate, measuring the moments of inertia accurately is more problematic.

3.2. Original Tyrannosaurus model

Table 3 shows the mass set results for Model 1. Additional mass sets for the entire tail, leg, limbless torso, body supporting itself on one leg while turning (for the turning biomechanical analysis), and body supporting itself on one leg (for the running biomechanical analysis) are included with the whole body and individual segment mass set data.

Data for the skeletal torso ( Fig. 5B , without B-spline solids or limbs; density of 1000 kg m ‒ 3) are not extremely different from our Model 1 torso estimates, as we started with a ‘skinny’ model that had a small amount of external flesh. The 3248 kg torso mass is 83% of Model 1. The CM (x; y; z) distance from the right hip is almost twice as far forward (1.10 m), more dorsal (‒ 0.089 m), and similarly medial (‒ 0.201 m). The principal inertia values about the CM (Ixx, Iyy, Izz of 730, 8810, and 9370 kg m 2) are 63–78% of Model 1.

3.3. Sensitivity analysis

Table 4 shows mass set data for all 30 of our Tyrannosaurus whole body models. As expected, the most dense model (#7; 894 kg m ‒ 3) has the largest torso segment and largest legs, and is the heaviest (8405 kg) model with the largest principal moments of inertia. Likewise, the least dense model (#21; 787 kg m ‒ 3) is also the lightest (5074 kg) and has the lowest principal inertia values; it is a combination of the smallest torso with the largest cavities.

The mediolateral position of the CM varies negligibly (always around 0.20 m medial to the right hip joint) whereas the dorsoventral position of the CM is closest to the hip (0.229 m ventrally) when the CM is furthest forward from the hip (0.744 m; Model 3 with the largest torso), and furthest from the hip (0.355 m ventrally) when the CM is in its most caudal position (0.453 m; Model 27 with enlarged legs and cavities). Inertia values vary less (3355–5880 kg m 2) for Ixx, relative to Iyy (11800– 19800 kg m 2) and Izz (14000–23700 kg m 2) but all vary within the same relative range (58–60%). All 26 other models occupy a continuum between the four most extreme models (#3,7,21,27). Our ‘best guess’ model (#30) lies in the middle of this continuum at 6583 kg total mass, CM 0.519 m cranial to the right hip, and moderate inertia values.

3.4. Turning ability

The time required for T. rex to turn to the right by 45 ° ranged from as slow as 2.2 s for the lowest joint moments and highest moments of inertia down to 1.3 s for the highest joint moments and lowest moments of inertia ( Table 7 ). The ‘best guess’ of turning time (moderate torque and inertia values) was 1.6 s. Neglecting the moment of inertia about the CM dramatically reduced the estimates of turning time, by a factor of 50% or less, as expected.

3.5. Running ability

We entered our best estimates of muscle moment arms ( Hutchinson et al., 2005) and mass set data (this study) into the mathematical model of Hutchinson (2004a, b), to estimate how big extensor muscles would need to be to support the forces of fast running, and how close these required muscle masses were to our estimates of actual muscle masses (from our models and scaled data from extant taxa). We found that the maximal vertical GRF supportable by the weakest link in the limb (the ankle, in all cases) ranged from 0.22–0.37 times body weight, which is far below the requirements of fast running (2.5 X body weight), or even standing. These unusual results are discussed further below.

4. Discussion

4.1. Body dimensions of Tyrannosaurus

The body dimensions of an adult T. rex have long been debated, with mass values ranging from 3400 to 10,200 kg ( Table 5 ), whereas only one set of studies has quantified the CM position and inertia for this animal ( Henderson, 1999; Henderson and Snively, 2003). Our body mass results (5074–8405 kg) overlap those of most studies, except those that use scaling equations from extant taxa (3458–4326 kg; Anderson et al., 1985; Campbell and Marcus, 1993). As many other studies have noted ( Alexander, 1985; Farlow et al., 1995; Paul, 1997; Carrano, 2001; Christiansen and Fariña, 2004) it is almost certain that these scaling equations greatly underestimate dinosaur body masses, especially for large bipeds. The data that the equations are based upon include no animals with body proportions (large head, small arms, long tail, bipedal and cursorial limbs, etc.) and size approaching those of large tyrannosaurs, so they are at a great disadvantage compared with estimates that directly use tyrannosaur body dimensions to estimate body mass. Hence, we recommend abandonment of their usage for large dinosaurs. This point is bolstered by our estimates of leg mass: their total mass in the ‘skinny’ Model 1 is 1552 kg (or 2266 kg for the largest legs). Total body mass must be much more than this value; at least 5000 kg. For example, the ‘skeletal’ torso mass alone (see Section 3) would add 3248 kg at 1000 kg m ‒ 3 density (= 4800 kg body mass) or 2477 kg with Model 1’s 763 kg m ‒ 3 torso density and the largest legs (= 4742 kg body mass), and these are surely underestimates of body mass as they were intentionally as skinny as we could plausibly construct the models.

Our lightest model (#21; original body with larger cavities) at 5074 kg is not very plausible as it seems greatly emaciated, and the torso cavities are quite tightly appressed to the skeletal landmarks, leaving little room for flesh or bone. Indeed, the former criticism applies to all 11 of our models with the torso volume in its original state, leaving us doubting our mass estimates that fall below about 6000 kg. Hence, we also are slightly skeptical about the low mass estimates obtained for MOR 555 by Paul (1997; 5360 kg) and lower-end results of Farlow et al. (1995; 5400 kg). Our models offer more plausible support for mass estimates of 6000+ kg ( Farlow et al., 1995; also assumed by Hutchinson and Garcia, 2002 and subsequent studies). Yet higher values such as Henderson’s (1999) estimates of ~ 7000+ kg seem equally plausible given the uncertainty about tyrannosaur body dimensions; our largest models (> 8000 kg) however seem to have an unrealistic amount of external flesh and so are less plausible. Henderson and Snively (2003) estimated the larger ‘‘Sue’’ Tyrannosaurus mass at 10,200 kg. Our ‘best guess’ Model 30’s mass (6583 kg) is 64.5% of that animal, but is for a smaller adult specimen, so it is not inconceivable that some large tyrannosaurs could have exceeded 10 tonnes (e.g., an individual with linear dimensions ~ 1.1 X ours). Additionally, differences in specimen (or reconstruction thereof) body length and other dimensions could account for some differences in body mass estimates, but these dimensions are seldom reported, rendering comparisons among studies difficult.

Hutchinson (2004b) calculated Tyrannosaurus ( MOR 555 ) limb segment masses from extant animal proportions, which provides an interesting comparison to our study’s results as our models were constructed blind to these data. The thigh segment in our study (500 kg) is ~ 1.2 X larger and the tibiotarsus segment (172 kg) is 61% of the mass scaling predictions, whereas the metatarsus segment mass estimate came surprisingly close at 62.8 kg (vs. 63 kg). Segmental CMs were generally fairly similar although our estimate for the thigh segment CM is much more proximal (0.162 m vs. 0.63 m). At 14.2% of body mass (19.7% in Model 27, with enlarged legs and cavities), our model’s legs are smaller than those of an ostrich or emu (19–27%; Hutchinson, 2004a). This is expected, as ratites differ from tyrannosaurs in having a relatively larger pelvis and longer limbs, more slender neck and tiny head, presumably larger (more derived) air sacs, and a miniscule tail (vs. 12.5% of body mass in Model 1, 15.0% in Model 30), even though ratites have a large herbivorous gut.

What density values are most realistic for tyrannosaur body segments? Our results suggest that a range of mean body density from 787–894 kg m ‒ 3 ( Table 4 ) is most appropriate. The anatomical evidence now strongly favors theropod torsos as being closer to the neornithine bird than the crocodilian condition ( Paul, 1988; O’Connor and Claessens, 2005; O’Connor, 2006) and hence having lower densities; using crocodilian lung anatomy as a guide to tyrannosaur dimensions is unreliable. Paul’s (1997) suggestion of a value of 850 kg m ‒ 3 falls comfortably within this range, as does our ostrich carcass measurement of 888 kg m ‒ 3 (albeit with presumably deflated air sacs). Models that assume homogeneous body densities of around 1000–1050 kg m ‒ 3 ( Colbert, 1962; Alexander, 1985; Henderson, 1999; Henderson and Snively, 2003) likely not only overestimate body mass but would also result in inaccurate CM positions and inertia values.

Alexander (2006:1849) infers that ‘‘[i]ncorrect assumptions about air sacs are unlikely to result in errors greater than 10%, in estimated dinosaur masses.’’ Our results concur with this, at least for air sacs up to ~ 46% larger than our initial model. However other parameters, especially position of the CM cranial to the hip, may incur more error—in Model 21, the CM cranial distance from the hip is 86% of Model 1’s even though density is only 93% of the original. Removing the abdominal air sac ( Fig. 7 ), whose presence is more ambiguous ( O’Connor and Claessens, 2005; O’Connor, 2006), increased the body mass for the ‘best guess’ model (#30) by 4% but the body CM position moved 8% craniad. Similarly, Tyrannosaurus had evidence of respiratory tissue being present as far caudally as the fourth sacral vertebra ( Brochu, 2003) hence (following O’Connor, 2006) our original model’s ‘‘lung’’ cavity might not have been caudally extensive enough, which would mean that some models (e.g., Model 1) might have CM values that are too far craniad. Thus information on air sac anatomical details is important although its effects on mass set parameters can often be small.

Our lower whole body density estimates of course resulted from fairly low densities for the body segments that contained cavities. For example, the trunk segment density (from pelvis to neck base) had values from 683 kg m ‒ 3 (Model 21) to 852 kg m ‒ 3 (Model 3). Our ‘‘lung’’ cavity occupied only 8.6% of the whole body volume (or 11.3% of torso volume) in Model 1 (slightly less in other models), up to 12.6% if the cavities were expanded by 1.46x (e.g., Model 21). However we also incorporated abdominal and tracheal cavities that brought the total trunk cavity volume to 11.6% body volume in Model 1 (17.0% in Model 21). Overall it seems unlikely that we have overestimated cavity volumes and hence underestimated density, as these volumes match those assumed in other studies and data from extant taxa fairly well (e.g., Alexander, 2006; Henderson, 1999, 2003a, b and references therein). Considering these data and the convergently avian-like respiratory system in sauropods ( Wedel, 2003, 2005), it is possible that Henderson (2003b) overestimated sauropod density, as sauropod trunk segment density (850 kg m ‒ 3 in that study; ~ 800 kg m ‒ 3 for the whole body) should be lower than our tyrannosaur values. Henderson (2006) used slightly lower values of ~ 800 kg m ‒ 3 for sauropod trunks.

Our models place the total body CM in front of (0.453–0.744 m) and well below (0.229–0.355 m) the hips ( Table 4 ). Larger legs or cavities or a larger tail (Models 28,30) move the CM closer to the hips and further ventrally. A 21% increase in two dimensions moved the CM furthest caudad for the tail (Model 28; by ‒ 0.13 m), moderately for the cavities (Model 21; by ‒ 0.085 m), and least for the legs (Model 23; by ‒ 0.066 m). Depressing the tail had smaller effects, confounded by a required increase of tail mass (CM moved 0.061 m caudad). If we have underestimated the dimensions of those structures, the actual CM of a Tyrannosaurus might have been slightly closer to the hips than 0.45 m craniad, but we doubt that it could have been closer than 0.40 m as none of our models approach that value—even considerable changes to tail (Model 28) or cavity (Model 21) anatomy do not shift the CM that far caudally. Model 30 represents the most plausible combination of larger tail, cavities, and legs, but we enlarged the body as we felt it was overly skinny, so the CM is still 0.51 m craniad to the hip (‒ 0.08 m from Model 1).

Our findings agree with what others have estimated for dinosaur CM positions (e.g., Alexander, 1985; Henderson, 1999): the CM lies a moderate distance in front of and below the hips—not directly at/underneath the hips like an ideal cantilever as dinosaurs are often described as in popular accounts. Yet, as noted above, our models show a moderate amount of variation in where the CM lies along the craniocaudal axis, which no other studies have emphasized. A body CM only 0.45 m cranial to the hips would require about 75% of the supportive hip antigravity muscle activity (or mass) relative to a CM 0.60 m cranial to the hips ( Henderson, 1999; Hutchinson and Garcia, 2002), so this variation has great biomechanical importance. We present more consideration of how different CM positions can influence limb muscle exertion below ( Table 6 ).

4.2. Turning ability of Tyrannosaurus

Accurate inertia data are crucial for estimating animal performance in turning and other accelerations, as Carrier et al. (2001) and Henderson and Snively (2003) have already shown for various theropods. The long tails and heavy bodies of theropods would have had high inertia about the y-axis (i.e., in yaw), and hence restricted their relative turning performance. This importance of inertia is reinforced by our estimates of turning times that neglect inertia ( Table 7 ). Yet no studies have addressed the pivotal question: How fast would turning performance be in absolute terms in a large theropod such as Tyrannosaurus ? Our estimate is a rather slow (~ 1–2 s) 45 ° turning performance.

However, we did not aim to present the final word on tyrannosaur turning performance. We kept our analysis simple in order to make a basic example of how whole body models can be combined with musculoskeletal models in order to examine locomotor performance in extinct animals, in conjunction with sensitivity analysis. More realistic additions to the analysis, such as laterally flexing the tail into the turn or using the opposite leg’s GRF in order to contribute to the total turning moment, would lower these turning times. Turning performance depends not only on rotating the body against its inertia, but also on the ability of the limbs to deflect the velocity heading of the CM to a new direction, which is related to musculotendinous ground-reaction force production, body mass, and CM position more than rotational inertia and muscle moments.

Nonetheless, we suspect that our basic conclusion is unlikely to change despite unavoidable inaccuracies in estimating mass sets and muscle moments: T. rex could not pirouette rapidly on one leg, as popular illustrations have sometimes pictured it and other large dinosaurs as doing (e.g., Bakker, 1986; Paul, 1988). Like our running performance estimates (below), this conclusion has little bearing on the tired media-based ‘debate’ over whether T. rex was a scavenger or predator. All of our models (and those of others such as Henderson and Snively, 2003) should apply quite well to the large dinosaurs (e.g., Edmontosaurus , Triceratops ) that T. rex likely preyed and scavenged upon. How turning capacity in bipeds vs. quadrupeds differs remains poorly understood by biomechanists (but see Usherwood and Wilson, 2005), so we do not yet consider this one potentially important difference. We would expect some turning performance differences betweeen the habitually quadrupedal Triceratops and the facultatively bipedal Edmontosaurus . Smaller dinosaurs likewise should have had relatively lower moments of inertia and relatively higher muscular moment-generating capacity. Hence, these animals would have been more agile in absolute terms.

4.3. Running ability of Tyrannosaurus

Recently, Hutchinson and Garcia (2002), Hutchinson (2004a, b), and Hutchinson et al. (2005) have confronted two related, longstanding questions about the paleobiology of large tyrannosaurs: what was the pose or limb orientation used by such animals during standing and moving, and the maximum running ability (if any) that these enormous bipeds had (for counterpoints see Paul, 1988, 1998). Because these questions are inherently biomechanical, we used biomechanics to address them, and hence we required estimations of body dimensions. Body mass was factored out of the analysis in Hutchinson and Garcia (2002) and Hutchinson (2004b), but the CM position entered into the biomechanical models was crucial, particularly for determining the hip extensor muscle mass needed for fast running. Inertia values were not incorporated into the latter studies; a more complex dynamic analysis is required to check the importance of inertia. We used our model to estimate the masses of hindlimb extensor muscles ( Table 8 ) and used these values to estimate running ability in Tyrannosaurus ( Table 9 ).

Considering that our models suggest a range of ~ 0.45–0.8 m in front of the hip for the body CM position during single-legged stance (similar to the few previous studies; Table 9 ), and moment arms can be bounded within a similarly narrow range for most hindlimb muscles ( Hutchinson et al., 2005), the largest two parameters of uncertainty for estimating running ability in Tyrannosaurus are the actual masses and fascicle lengths of extensor muscles. Our models bounded the likely masses ( Table 8 ) of hip extensors in the range of 5–10% body mass, whereas knee and ankle extensors fall well under 5% (1.5–4.1%); totaling 9.6–14.2% body mass per leg. These are plausible results, as the largest extensor muscles known in living animals are in ratites (14–15% body mass total; Hutchinson, 2004a) and there is no convincing anatomical evidence that Tyrannosaurus had relatively larger muscles (see above). Furthermore, our models had legs totaling up to 19.7% of body mass (not counting tail-based hip extensors) so total muscle masses must be well below this value.

Our estimates of maximal GRF supportable on one limb (~ 0.3 X body weight; Table 9 ) fall very low, as absolute muscle masses needed for running are as high as 17% for single joints (i.e., the ankle) and totaling 24–30% body mass. The GRF values are for a fairly flexed limb pose, so they would be increased by up to 4 X (bringing them over 1 X body weight) in more upright poses ( Hutchinson, 2004b). However, our model results lead us to suspect that our estimates of extensor muscle fascicle lengths (see Section 2 and Hutchinson, 2004b), which are inversely proportional to maximal GRF values, are still too high. Thus, to improve reconstructions of dinosaur running ability, more analysis is most needed to narrow down the possible ranges of values for limb muscle fascicle lengths. The error is unlikely to be more than 2x, however, as much lower values would reduce the fascicle lengths to be equal to or smaller than the values seen in large extant bipeds ( Hutchinson, 2004a), which is extremely unlikely. An additional likely source of error is the lower leg segment masses, as a 2x factor of error is not implausible and would increase muscle masses proportionately. So far, fossil bones do not help to further constrain these parameters.

Regardless, our amended parameter values only alter the conclusions of previous biomechanical studies quantitatively, not qualitatively—the muscle masses needed for fast running are still be too high (over 5–9% of body mass per leg), as Table 9 shows.

5. Conclusions

There is no question that careful sensitivity analysis of unknown body dimensions in modeling the biomechanics of extinct vertebrates is important, and we have conducted the most detailed such study for any one extinct taxon. Sensitivity analysis can also identify which mass parameters are relatively stable or which parameters are sensitive. This can help researchers to prioritize where to focus their efforts to get more accurate measurements, or to identify which parameters might be negligible and therefore not worth the modeling effort. The method we have developed here facilitates sensitivity analysis by making it relatively easy to model slight deviations of shape or different scenarios and quickly seeing their effect on the mass estimates.

We also have aimed to demonstrate how estimates of extinct animal body dimensions can be used in a biomechanical analysis and uncover stimulating results, revealing the likely slow absolute (as opposed to relative; Carrier et al., 2001; Henderson and Snively, 2003) turning performance of large theropods and its high dependence on the body moments of inertia. By providing more realistic estimates of body dimensions, we strengthen the conclusions of Hutchinson and Garcia (2002) and Hutchinson (2004b), emphasizing why T. rex should not have been a fast runner. Together with our inertia estimates (also moment arms from Hutchinson et al., 2005), these studies continue to support the inference that it used a more upright pose than some have assumed (e.g., Bakker, 1986; Paul, 1988, 1998). However, our CM estimates reinforce the conclusions of Hutchinson et al. (2005) that the limb was not completely columnar as in a standing elephant: in order to bring the foot under the CM (at least 0.4 m in front of the hip) and the knee in front of the CM (Hutchinson and Gatesy, 2006), the limb must have had some flexion. Whether this degree of flexion is similar to that argued by other studies (e.g., Paul, 1998; Christiansen, 1999) depends on the CM value and what is specifically meant by ‘flexed’ (see Hutchinson et al., 2005).

Certainly no estimate of body mass, CM, or moments of inertia for extinct animals will ever be very accurate, as it would be hubris to expect that any model will match the real animal. We have our own misgivings about the accuracy of our Tyrannosaurus model despite its improvements over other models—in the future we could improve our representations of the arms/chest, or leg/tail shape and orientation, for example, particularly with higher-resolution data for well-preserved skeletal elements. As little is knowable about the soft tissue dimensions and densities of Tyrannosaurus , we might never obtain much narrower estimates than in this study. The question should always be, then, is any estimation accurate enough for a higherlevel inference to be based upon it? This will depend on the research question (e.g., how did a dinosaur move, as in this study). Sensitivity analysis is a step that always should follow the presentation of a numerical result as a conclusion of such a study. Without investigation of how the question is affected by potential error in mass parameter estimates, the strength of any conclusion is uncertain. Studies assuming one numerical result for mass parameters without checking the effects of possible error on their numerical results and hence the conclusions based upon them should be viewed warily. Many studies obtain only one estimated value for body dimensions of interest. Thereafter that value is typically treated as a known parameter, without checking the effects of potential error on the conclusions. Or, only a brief sensitivity analysis is conducted, without considering that a unconsidered but plausible value for an unknown parameter such as CM position might greatly change the conclusions.

Our analysis has showed how sensitive some body mass parameters are to the assumptions about body form. Even slight changes in size, shape, or density can substantially alter CM position or moments of inertia—especially if these changes occur far from the CM, such as in the tail (e.g., our Model 28). Conversely, changes of body form close to the CM, such as in the trunk or legs of a biped, often have small or even negligible effects on some mass parameters. Our Models 7 (large body and legs) and 27 (small body, large legs, and cavities) demonstrate these basic facts of geometry and rigid body dynamics. Yet neither case always necessarily holds. The effects of minor alterations of geometry on system dynamics can be nonintuitive. Models 11 and 17 ( Table 4 ) have cranial CM positions similar to Model 1 despite different anatomy, but have very different mass and inertia parameters. Modeling anatomical aesthetics with our mass set approach can quantitatively determine if anatomical features of interest have a direct effect on the mass parameters. Our point is these potential effects must be investigated cautiously, and their implications phrased in the context of the bigger question being addressed. Estimating the body mass parameters of extinct animals is not important in and of itself. It becomes important when used to test a question, and then the accuracy of that estimation becomes vital to address.

Figures

Fig. 2. A B-spline solid is a closed object whose shape can be adjusted by moving control points (dark points) that deforms the local portion of the object near the control point. The initial cylindrical shape in A is adjusted (B and C) by pulling out the points at the ends and drawing the points in the middle closer to the axis.

Fig. 5. Tyrannosaurus MOR 555 skeleton: (A) Photograph of mounted skeleton in Berkeley, California (in left lateral view); (B) Torso skeletal landmark points digitized for our study, plus digitized pelvis and leg bones from Hutchinson et al. (2005); and (C, D) additional cranial and caudal photographic views of the skeleton from A.

Fig. 6. Original Tyrannosaurus mass set (Model 1) in right lateral (A), dorsal (B), cranial (C), caudal (D), and oblique right craniolateral (E) views. Not to scale. The odd shape of the hip region in (B) represents the 15° adbuction of the thigh segment (see Section 2), which makes the thigh seem laterally-flared in dorsal view. This is also evident in the abducted positions of the lower legs and feet in C–E. It is not yet clear precisely how theropod dinosaur hindlimb joints (especially the hip and knee) brought the feet close to the body midline (e.g., Paul, 1988; Hutchinson et al., 2005), so our model was left with its feet in an abducted position (making it easiest to edit 3D leg dimensions), which had no important effects on our results.

Fig. 7. The six cavities embedded in Tyrannosaurus Model 1’s head, neck, and trunk segments, shown in right lateral (A) and dorsal (B) views. ‘bc’ indicates the buccal cavity; and ‘pc’ indicates the pharyngeal cavity.

Fig. 8. Six Tyrannosaurus models (in right lateral view) from our sensitivity analysis, representing the extreme high and low values obtained for mass, CM, and inertia. Shown: Model 1 (original ‘skinny’ model), Model 3 (largest torso), Model 7 (largest torso and legs), Model 21 (largest cavities), Model 27 (largest legs and cavities), and Model 30 (‘best guess’). The right hip joint (pink circle; to left) and total body COM with respect to that point (red circle; to right) are indicated, with the x; y; z world axes (right hip joint) and the x; y; z principal axes for inertia calculations (COM) indicated by arrows.

Fig. 9. Mass sets used for the Tyrannosaurus turning body analysis; shown for Models 1, 30, and 3.

Fig. 1. Body segments can be created using mass objects of different density and shape. Mass objects can be collected into mass sets to calculate their combined inertial properties; the most inclusive Tyrannosaurus mass set (whole body) is outlined here, as well as the trunk segment and its embedded mass objects.

To illustrate the importance of moment of inertia in dynamic movements, we estimated the minimum time required for T. rex to execute a stationary turn of its trunk, neck, and head by 45 ° to the right (clockwise) while standing only on its right foot. We assumed that the tail during this movement would not move with the trunk. Therefore, the turning mass set included the trunk starting from just behind the pelvis at the base of the tail, the left hindlimb, the neck, and the head ( Fig. 9 ). We further assumed that the optimal strategy for a minimum-time turn (to the right) would be to turn the right medial (internal) rotator muscles on maximally to initiate the turn and then the right lateral (external) rotators on for decelerating the turn to a stop at the final angle. The T. rex began at rest in a forward facing position (O i = 0:0 Q; ̇O i = 0: 0 Q / s) and terminated facing 45 ° to the right also at rest (O f = 45:0 Q; ̇ O f = 0:0 Q / s). Allowing for the fact that the maximal medial rotation and lateral rotation hip joint moments were not likely the same, a formula for the time required by the movement is given by where tturn is the time it takes to execute the turn, O f is the final medial rotation angle of the right hip, T med and T lat are the estimated maximum medial and lateral hip joint moments, respectively, that can be generated by T. rex , and Iyy is the moment of inertia of the rotating body mass about the right hip joint.

Tables

Table 3 Results for the original Tyrannosaurus body model

Segment	Density (kg m‒ 3)	Volume (m3)	Mass (kg)	CM (x, y, z) (m)	I, I, I(kg m2) xx yy zz
Head	650	0.534	347	(0.484, 0.193, ‒ 0.006)	(38.5, 53.1, 64.2)
Buccal cavity	0	0.120	0	n/a	n/a
Sinus	0	0.0667	0	n/a	n/a
Neck	724	0.228	165	(0.253, 0.652, ‒ 0.002)	(19.1, 8.67, 20.0)
Pharyngeal cavity	0	0.0623	0	n/a	n/a
Trunk	783	3.46	2708	(0.986, ‒ 0.281, ‒ 0.201)	(735, 2390, 2810)
Trachea	0	0.0263	0	n/a	n/a
Lungs	0	0.554	0	n/a	n/a
Abdominal sacs	0	0.168	0	n/a	n/a
Thigh	1000	0.500	500	(‒ 0.016, ‒ 0.162, 0.204)	(153, 42.9, 175)
Shank	1000	0.172	172	(0.016, ‒ 0.670, 0.102)	(20.5, 5.94, 20.9)
Metatarsus	1000	0.0628	62.8	(‒ 0.005, ‒ 0.418, 0.114)	(3.31, 1.95, 2.94)
Pes	1000	0.0410	41.0	n/a	n/a
Tail 5 (base)	1000	0.563	563	(‒ 0.636, 0.819, 0.000)	(56.8, 122, 162)
Tail 4	1000	0.0608	60.8	(‒ 0.354, 0.281, 0.000)	(1.03, 3.03, 3.69)
Tail 3	1000	0.0450	45.0	(‒ 0.455, 0.240, 0.000)	(0.473, 4.33, 4.67)
Tail 2	1000	0.00854	8.54	(‒ 0.288, 0.173, 0.000)	(0.036, 0.349, 0.379)
Tail 1 (tip)	1000	0.00124	1.24	(‒ 0.230, 0.091, 0.000)	(0.001, 0.039, 0.040)
Multiple segment groups:
Tail	1000	0.68	679	(‒ 1.801, ‒ 0.0970, ‒ 0.219)	(69.4, 526, 578)
One leg	1000	0.78	776	(0.007, ‒ 0.750, ‒ 0.288)	(773, 65.1, 784)
Limbless body	796	4.90	3899	(0.823, ‒ 0.116, ‒ 0.204)	(1150, 11,300, 12,000)
Turning body	800	5.00	3996	(1.121, ‒ 0.270, ‒ 0.285)	(2150, 6390, 7890)
Right leg support	823	5.68	4674	(0.693, ‒ 0.217, ‒ 0.276)	(2300, 11,900, 13,500)
Whole body	845	6.45	5450	(0.599, ‒ 0.289, ‒ 0.199)	(3460, 12,400, 14,800)

The CM column lists the x, y, and z distances of the segment CM, which is from the base (caudal end for head and neck; cranial end for tail) of the segment, from the proximal joint center for the limb segments, or from the right hip joint center for the trunk and all multiple segment groups.

Table 4 Alternative body models of Tyrannosaurus for comparison with the original (Table 3)

Model	Torso (y, z)	Legs (x, z)	Cavities (y, z)	Density (kg m2)	Mass (kg)	Ratio	CM (x, y, z) (m)	I, I, I(kg m2) xx yy zz
1	Original	Original	Original	845	5450	1.00	(0.599, ‒ 0.289, ‒ 0.199)	(3460, 12,400, 14,800)
2	+10%	Original	Original	867	6479	1.19	(0.678, ‒ 0.257, ‒ 0.199)	(4020, 15,500, 18,200)
3	+21%	Original	Original	886	7723	1.42	(0.744, ‒ 0.229, ‒ 0.199)	(4800, 19,200, 22,400)
4	+10%	+10%	Original	872	6788	1.25	(0.647, ‒ 0.279, ‒ 0.198)	(4500, 15,800, 18,800)
5	+10%	+21%	Original	878	7161	1.31	(0.613, ‒ 0.304, ‒ 0.197)	(5080, 16,100, 19,400)
6	+21%	+10%	Original	890	8032	1.47	(0.716, ‒ 0.249, ‒ 0.198)	(5290, 19,500, 23,000)
7	+21%	+21%	Original	894	8405	1.54	(0.684, ‒ 0.271, ‒ 0.198)	(5880, 19, 800, 23, 700)
8	+10%	+10%	+21%	824	6411	1.18	(0.582, ‒ 0.289, ‒ 0.198)	(4410, 15,200, 18,100)
9	+10%	+21%	+21%	832	6785	1.24	(0.550, ‒ 0.314, ‒ 0.197)	(4980, 15,400, 18,700)
10	+10%	+10%	+10%	850	6617	1.21	(0.618, ‒ 0.284, ‒ 0.198)	(4460, 15,500, 18,500)
11	+10%	+21%	+10%	857	6991	1.28	(0.585, ‒ 0.308, ‒ 0.197)	(5040, 15,800, 19,100)
12	+21%	+10%	+21%	848	7655	1.40	(0.665, ‒ 0.256, ‒ 0.198)	(5200, 18,900, 22,400)
13	+21%	+21%	+21%	854	8029	1.47	(0.634, ‒ 0.279, ‒ 0.197)	(5790, 19,300, 23,100)
14	+21%	+10%	+10%	871	7861	1.44	(0.693, ‒ 0.252, ‒ 0.198)	(5260, 19,200, 22,700)
15	+21%	+21%	+10%	876	8235	1.51	(0.662, ‒ 0.275, ‒ 0.197)	(5840, 19,600, 23,400)
16	+10%	Original	+10%	844	6309	1.16	(0.649, ‒ 0.261, ‒ 0.199)	(3980, 15,300, 17,900)
17	+10%	Original	+21%	816	6103	1.12	(0.611, ‒ 0.266, ‒ 0.199)	(3930, 14,900, 17,600)
18	+21%	Original	+10%	866	7553	1.39	(0.721, ‒ 0.232, ‒ 0.199)	(4770, 19,000, 22,200)
19	+21%	Original	+21%	843	7347	1.35	(0.693, ‒ 0.235, ‒ 0.199)	(4720, 18,700, 21,800)
20	Original	Original	+10%	819	5280	0.97	(0.562, ‒ 0.295, ‒ 0.199)	(3410, 12,100, 14,400)
21	Original	Original	+21%	787	5074	0.93	(0.514, ‒ 0.302, ‒ 0.199)	(3360, 11, 800, 14, 000)
22	Original	+10%	Original	852	5759	1.06	(0.567, ‒ 0.314, ‒ 0.198)	(3920, 12,700, 15,300)
23	Original	+21%	Original	857	6113	1.12	(0.533, ‒ 0.340, ‒ 0.197)	(4490, 12,900, 15,900)
24	Original	+10%	+10%	827	5589	1.03	(0.531, ‒ 0.320, ‒ 0.198)	(3880, 12,400, 14,900)
25	Original	+10%	+21%	797	5383	0.99	(0.484, ‒ 0.328, ‒ 0.198)	(3830, 12,000, 14,500)
26	Original	+21%	+10%	836	5962	1.09	(0.498, ‒ 0.347, ‒ 0.197)	(4450, 12,600, 15,500)
27	Original	+21%	+21%	807	5757	1.06	(0.453, ‒ 0.355, ‒ 0.197)	(4390, 12,200, 15,100)
28	Tail+21%	Original	Original	852	5765	1.06	(0.467, ‒ 0.268, ‒ 0.204)	(3570, 14,400, 16,800)
29	Ventral tail a	Original	Original	849	5597	1.03	(0.538, ‒ 0.333, ‒ 0.199)	(3355, 13,300, 15,500)
30	Body/tail b	10%	21%	827	6583	1.21	(0.519, ‒ 0.279, ‒ 0.201)	(4470, 16,300, 19,200)

Torso and leg segments as well as internal cavities were enlarged or reduced by specified percentages along the axes indicated in parentheses. The ratio column shows the total body mass relative to Model 1. The CM column lists the x, y, and z distances of the whole body (including both legs) CM from the right hip joint center. For density, mass, CM, and inertia the largest and smallest values are, respectively, indicated by bold and italic fonts.

a The tail in Model 29 is ventrally depressed by ~ 25 ° and slightly enlarged (see Section 2).

b Model 30 represents our ‘best guess’ at reasonable mass set values, with the body dimensions enlarged 10% and tail dimensions enlarged 21%.

Table 6 Assumed input parameters for estimating turning times of Tyrannosaurus

	Joint moments		Inertial	parameters
	T med (N m)	T l at (N m)	m (kg)	rcom (m)	I com (kg m2) yy	m r 2 (kg m2) com	I com + m r 2 (kg m2) yy com
Low	10,000	25,000	3996	1.121	6390	5022	11,412
Med	13,000	31,000	4669	1.160	7915	6283	14,198
High	16,000	37,000	5972	1.263	9750	9526	19,276

Low (Model 1), medium (Model 30), and high (Model 3) estimates of maximal medial and lateral rotation muscle moments are shown. The mass m, r(distance of the CM along the x -axis from the right hip joint), and inertia (I com) are for the body (counting the left hindlimb) forward of the tail com yy base ( Table 3 : turning body segment group; Fig. 9 ).

Table 8 Calculation of approximate Tyrannosaurus hindlimb extensor muscle masses from total leg segment masses, using data from extant taxa (Hutchinson, 2004a)

Model	Original (Model 1)	Large cavities (Model 21)	Large leg (Model 23)	Best guess (Model 30)
Mass (kg)
Body	5450	5074	6113	6583
Thigh	500	500	733	605
Shank	172	172	251	208
Meta	62.8	62.8	91.9	49.2
Extensor muscle mass/segment mass
Extant taxa: Non-avian		Avian	Both
Hip	0.68	0.41	0.54
Knee	0.19	0.34	0.26
Ankle	0.37	0.57	0.47
Estimated extensor muscle mass (kg)
Hip	271	271	398	328
Knee	171	171	251	207
Ankle	81	81	119	98
Muscle % body mass
Hip	5.0 (7.6)	6.5 (8.8)	5.4 (8.1)	5.0 (9.6)
Knee	3.1	3.4	4.1	3.1
Ankle	1.5	1.6	1.9	1.5
Total	9.6 (12.2)	11.5 (13.8)	11.4 (14.1)	9.6 (14.2)

Values of extensor muscle mass/segment mass in bold are those used in the calculations below them in this table.

Hip muscle masses in parentheses indicates values with the hip muscle mass increased by 1/4 of the tail base (tail segment5) mass, to represent added caudofemoral extensor musculature.

Table 9 Calculation of the hindlimb extensor muscle masses required for Tyrannosaurus to run with a ground reaction force (GRF) of 2.5 times body weight (BW)

Model	Mass (kg)	CM (x, y) (m)	Extensor muscle masses required (% body mass)				Max GRF (BW)
			Hip	Knee	Ankle	Total
Trex_1 ( Hutchinson, 2004b)	6000	(0.585, 0.0)	9.7	2.7	8.3	20.7	1.8
Original (Model 1)	5450	(0.693, ‒ 0.217)	10	2.4	13	25.4	0.29
Model 1 with folded limb	5450	(0.801, ‒ 0.147)	13	n/a	17	30.0	0.22
Large air sacs (Model 21)	5074	(0.601, ‒ 0.225)	10	4.2	13	27.2	0.37
Large legs (Model 23)	6113	(0.645, ‒ 0.225)	9.8	2.8	12	24.6	0.33
‘‘Best guess’’ (Model 30)	6583	(0.600, ‒ 0.204)	10	2.9	12	24.9	0.31

Body dimensions are taken from the models in Table 4 . CM positions are for single-legged support (as in Hutchinson, 2004a, b) and are relative to the right hip joint. The extensor muscle masses are for one limb; bold values indicate the highest value for a given model (and hence potentially the weakest joint in the limb). The final column ‘‘Max GRF’’ shows what peak vertical GRF (in multiples of body weight) the limb could sustain under maximal exertion; see Section 2 for explanation.

Table 2 Mass sets for the ostrich from experimental measurements (REF) and the three models from this study

Method	Mass (kg)	Mass (kg)-corrected	CM (x, y, z) (m)	I(kg m2) xx	I(kg m2) yy	I(kg m2) zz
Experiment	34.9		(0.081, ‒ 0.167, ‒ 0.098)	0.397	0.892	1.45
Carcass model	39.3	34.9	(0.063, ‒ 0.139, ‒ 0.052)	0.375	1.53	1.75
Skeleton model	29.2		(0.096, ‒ 0.106, ‒ 0.061)	0.282	1.39	1.49
Fleshed-out model	39.1	34.7	(0.098, ‒ 0.112, ‒ 0.060)	0.377	1.887	2.045

The CM column lists the x, y, and z distances of the trunk CM from the right hip joint center. Bold values for the mass set parameters indicate closest matches to the experimental measurements.

Table 7 Estimated times in seconds for a Tyrannosaurus to turn to the right by 45° while standing on one leg

	Ihigh	Imed	Ilow
T low	2.2 (1.4)	1.8 (1.2)	1.6 (1.0)
T med	2.0 (1.3)	1.6 (1.0)	1.4 (0.90)
T high	1.8 (1.2)	1.4 (0.94)	1.3 (0.84)

Joint moment and inertial input parameters for Eqs. (10) and (11) are listed in Table 6 . Numbers in parentheses are for when the moment of inertia about the CM of the turning mass set is neglected (i.e., I com = 0:0 in yy Table 6 ).

Table 5 Comparison of our mass set estimates with those of other studies

Study	Mass (kg)	CM (x, y, z) (m)	I, I, I(kg m2) xx yy zz
Colbert (1962)	6890/7700	n/a	n/a
Alexander (1985)	7400	n/a a	n/a
Anderson et al. (1985)	4028b	n/a	n/a
Campbell and Marcus (1993)	3458b	n/a	n/a
Paul (1987)	5700	n/a	n/a
Paul (1997)	5360b	n/a	n/a
Farlow et al. (1995)	5400–6300b	n/a	n/a
Henderson (1999)	7224/7908	(0.59, 0.25, n/a)a	n/a
Christiansen (1998,1999)	6250–6300c	n/a	n/a
Seebacher (2001)	6650.9	n/a	n/a
Henderson and Snively (2003)	10,200	n/a	(n/a, 35,150, n/a)
Our original model (#1)	5450b	(0.599, ‒ 0.289, ‒ 0.199)	(3460, 12,400, 14,800)
Our ‘‘best guess’’ model (#29)	6583b	(0.519, ‒ 0.279, ‒ 0.201)	(4470, 16,300, 19,200)

CM locations are relative to the right hip joint center.

a Indicates that the CM location was not quantitatively stated; in one reference it was estimated from the figures.

b Indicates that the mass estimate is for the same Tyrannosaurus specimen ( MOR 555 ), either from modeling or scaling equations.

c Notes that similar results were obtained by Christiansen and Fariña (2004).