Tillancoccus koreguajae Caballero & Ramos
|
publication ID |
https://doi.org/10.11646/zootaxa.4258.5.6 |
|
publication LSID |
lsid:zoobank.org:pub:EA2A1731-E70D-4EC5-81D0-32F793CB3BF0 |
|
DOI |
https://doi.org/10.5281/zenodo.6017805 |
|
persistent identifier |
https://treatment.plazi.org/id/D031854D-FFBE-FF9D-FF66-4B7D5E7FE00F |
|
treatment provided by |
Plazi |
|
scientific name |
Tillancoccus koreguajae Caballero & Ramos |
| status |
sp. nov. |
Tillancoccus koreguajae Caballero & Ramos , sp. nov.
Material studied. Holotype: adult female. Colombia: Caquetá, Florencia , Vda. San Luis, 388 m a.s.l., 01°41′01″N, 75°37′42″W, 11.x.2013, Coll. A. Caballero, ex leaves of sugarcane, S. officinarum , associated with Pheidole sp. ( Hymenoptera : Formicidae ), UNAB voucher N° 836. Paratypes: collection data same data as holotype, 1 adult female + 2 third-instar female nymphs. Only slide mounted specimens are available. Males not observed. GoogleMaps
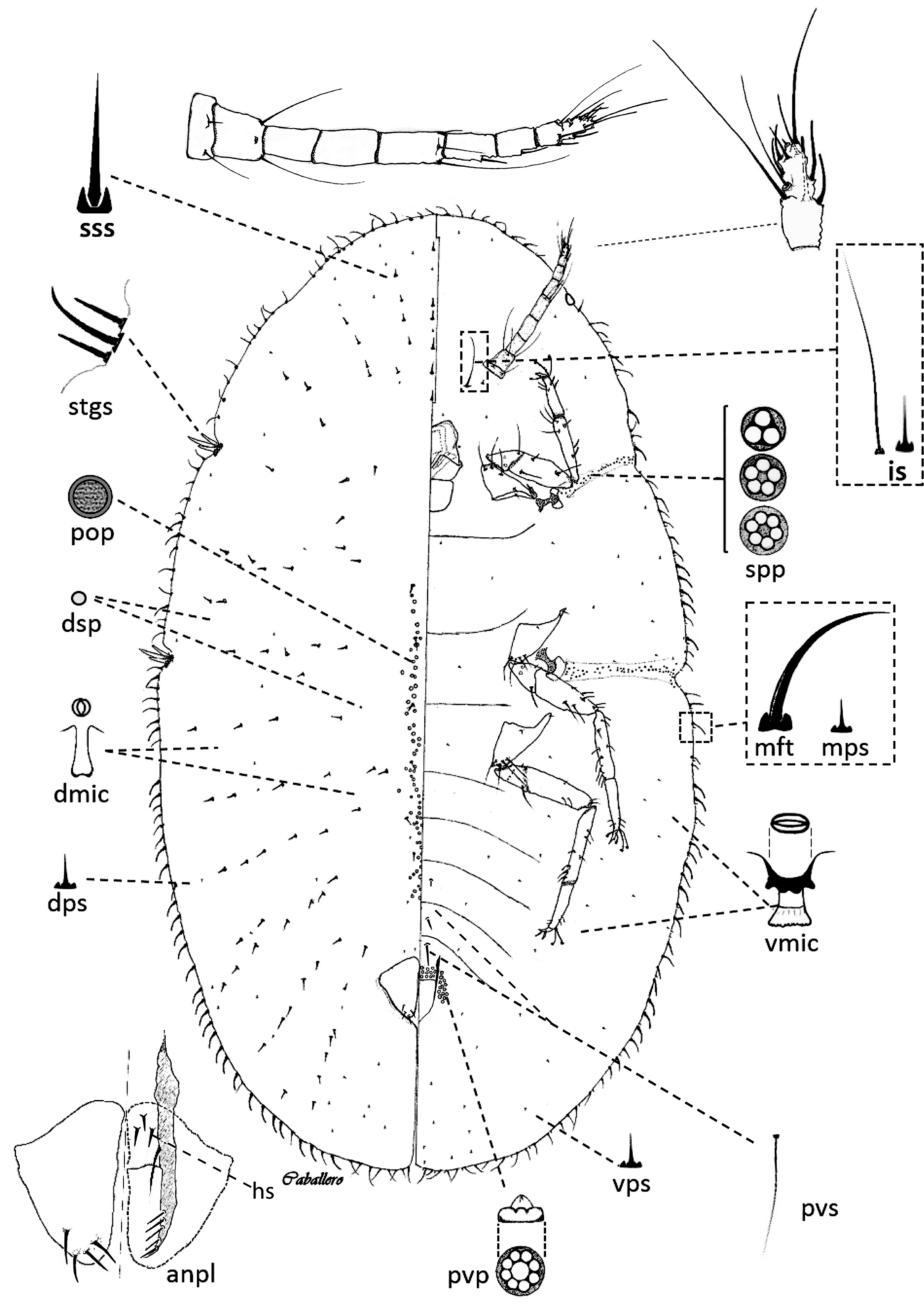
Description of adult female ( Fig. 1 View FIGURE 1 )
Note: data in brackets refer to the paratype female.
Mounted material. Body broadly oval, 2.1 (3.9) mm long and 1.2 (2.6) mm wide. Stigmatic clefts shallow, distinct. Anal cleft about 1/5 body length.
Dorsum. Derm membranous, except for a slightly sclerotized area around anal plates. Anal ring with 8 setae and two rows of wax pores. Anal plates (anpl) together subquadrate; each anal plate 138 (149) µm long, 86 (86) µm wide, anterolateral-margin 99 (104–106) µm long, posterolateral margin 114 (123–124) µm long, with 4 dorsal setae located on posterior end of each plate. Ducts: tubular ducts absent. Dorsal microducts (dmic) each 1.5 µm wide, evenly scattered throughout. Pores: Dorsal simple pores (dsp) each 1–2 µm wide, evenly scattered. Preopercular pores (pop) arranged in two rows on mid-dorsum anterior to anal plates, extending anteriorly up to middle of mesothorax, numbering 132 (109); each row 2–3 pores wide, each pore 6–8 µm wide. Setae: two types: a) sharply spinose setae (sss), large, each 23–36 µm long, with a narrow and well-sclerotized basal socket, arranged in about 25 radial rows as follows: seven radial rows present anteriorly between anterior stigmatic clefts on head; two to four (often not well-defined) radial rows between each anterior and posterior stigmatic cleft, and 12 radial rows present posteriorly between posterior stigmatic cleft and body apex; b) small pointed setae (dps), very short, slender, straight, 3–5 µm long, scattered. Dorsal tubercles and pocket-like sclerotizations absent.
Venter. Derm entirely membranous. Eyes present on margin, each about 24 (27) µm in diameter. Antennae slender, filiform, eight segmented, 335 (391) µm long, length of each segment as follows: I: 34 (37) µm, with 2 flagellate setae; II: 48 (59) µm, with 2 flagellate setae and one campaniform sensillium; III: 44 (51) µm, without setae; IV: 45 (53) µm, without setae; V: 52 (73) µm, with 3 flagellate setae; VI: 33 (43) µm, with 1 fleshy seta; VII: 31 (29) µm, with 1 fleshy seta and VIII: 45 (44) µm, with 4 fleshy setae, 4 stiff setae and 4 flagellate setae. Legs well developed; hind leg measurements as follows: coxa 97 (116) µm long, 94 (110) µm wide; trochanter 83 (96) µm long, 46 (57) µm wide; tibia 169 (212) µm long, 30 (30) µm wide; tarsus 108 (137) µm long, 26 (32) µm wide; claw 29 (30) µm long; claw denticle absent, claw digitules each about 28 (28) µm long, knobbed; tarsal digitules each about 55 (56) µm long, knobbed. Spiracles well developed, anterior spiracles each 46 (57) µm wide, posterior spiracles each 54 (61) µm wide. Tubular ducts absent. Ventral microducts (vmic) about 3 µm wide, evenly scattered throughout. Pores: Perivulvar pores (pvp), each 5–7 µm wide, with 5–7 loculi (mostly 7), present only around vulvar region. Spiracular pores (spp) each 4–5 µm wide, with 5 loculi, present in a narrow band 2–3 pores wide, extending laterally from each spiracle to body margin, numbering 40–50 pores on each furrow. Setae: i) interantennal setae (is): two pairs, one pair of long flagellate setae, each 74 (56) µm long, and one pair of shorter hair-like setae, each 7 (7) µm long; ii) prevulvar setae (pvs) hair-like, present on last three abdominal segments: one pair on mid region of segment V, each 13 (18) µm long, one pair on mid region of segment VI, each 15 (19) µm long, and one pair on mid region of segment VII, each 59 (89) µm long; iii); and a iv) short type of setae herein termed as ventral pointed setae (vps): very short, slender, straight, about 3–5 µm long, evenly scattered. Dermal spinules present on medial and submedial areas of body, between base of antennae and the anal cleft.
Margin. Setae of two types: i) flagellate setae (mfs), slightly bent, each 28–46 (25–50) µm long, arranged in a single row, with 23 (24) setae anteriorly between the eyes, 11 (10) between each eye and anterior stigmatic setae on each side, 15 (11) between anterior and posterior stigmatic spines on each side, 47–49 (42–51) setae between each posterior stigmatic setae and body apex on each side; intermixed with ii) pointed setae (mps), very short, slender, straight, about 3–5 µm long, similar to ventral pointed setae. Stigmatic cleft well developed, with 3 stigmatic spines per stigmatic area; stigmatic spines (stgs) each sharply spinose, median stigmatic spine longest, 63–69 (80) µm long (one seta bifurcated on anterior stigmatic cleft on right side in paratype), lateral stigmatic spines 27–46 (52– 58) µm long.
Etymology. The species is named in honor of the Colombian native tribe from the Type locality, the Koreguajae ( Marin 2013) , a noun in apposition.
Tillancoccus koreguajae is most similar to Tillancoccus tillandsiae in having the same type of dorsal setae and in lacking dorsal tubercles and dorsal setae with associated pores (present in T. mexicanus ); however, the two species differ in the number of rows of setae on the dorsum, number of antennal segments, and the number of loculi in the spiracular pores. Tillancoccus tillandsiae differs from the other two species in the presence of very short and slender pointed setae, which have not been reported in either T. tillandsiae or T. mexicanus . Differences between Tillancoccus koreguajae from the other two known species in the genus (i.e., T. mexicanus and T. tillandsiae ) are summarized in Table 1.
Characters Attribute
| UNAB |
Universidad Nacional, Facultad de Agronomia |
No known copyright restrictions apply. See Agosti, D., Egloff, W., 2009. Taxonomic information exchange and copyright: the Plazi approach. BMC Research Notes 2009, 2:53 for further explanation.
|
Kingdom |
|
|
Phylum |
|
|
Class |
|
|
Order |
|
|
Family |
|
|
Genus |